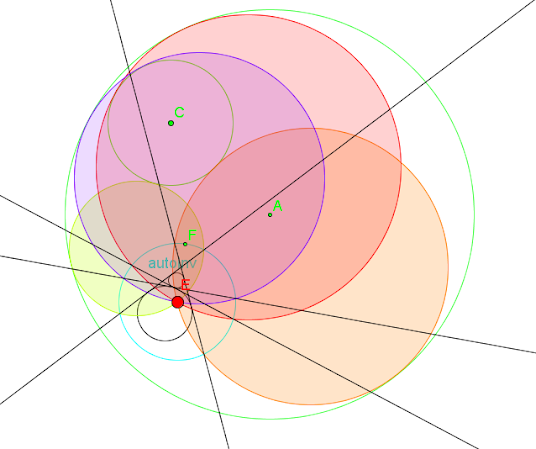
Tal y como tenemos en el dibujo, una recta verde y una recta ocre, consideramos un punto aleatorio CR como centro de inversión así como una circunferencia de autoinversión -en color gris- de un radio cualquiera, y construimos las inversas a las dos rectas, que son la circunferencia verde y siena, respectivamente.
Construimos las tangentes comunes a ambas (rectas magentas) y a continuación dibujamos las inversas de las dos rectas, éstas son en realidad las circunferencias tangentes a las rectas dadas y que al mismo tiempo pasan por el centro de inversión CR.
-----------------------------------------------------------------------------------------------------
Tomamos un punto cualquiera como centro de inversión, por ejemplo CR, y una circunferencia cualquiera como de autoinversión -en color azul "auto".
Dibujamos las inversas de ambas circunferencias obteniendo las dos circunferencias correspondientes, a las que hacemos las tangentes comunes (en color verde). Las dos circunferencias grises CR-M-N y CR-K-L inversas de las circunferencias anteriores y que pasan por el centro de inversión son las tangentes a las circunferencias dadas.
16- Tras estos dos ejemplos podemos comprobar el procedimiento para resolver ejercicios de tangencias mediante inversión, acabamos de verificar que efectivamente las inversas de las tangentes de las inversas de los datos son los elementos tangentes a los datos, es por lo que debemos seguir los siguientes pasos:
-----------------------------------------------------------------------------------------------------
Es un problema elemental que no se hace mediante inversión, bastaría con unir los tres puntos dados mediante dos segmentos a los que se le hace sus mediatrices, la intersección de ambas es el centro de la circunferencia.
1- Escoger un punto C de los datos como centro de inversión y cualquier radio para la circunferencia de autoinversión (en color siena).
2- Hacer las inversas de los datos. Los puntos AB se transforman mediante inversión en A'B'
3- Hacer las tangentes comunes a las inversas. Un punto es como una circunferencia muy pequeña, por tanto las tangentes a dos circunferencias se convierten en una recta m que pasa por los dos puntos.
4- Hacer las inversas de las tangentes. la inversa de la recta m es la circunferencia que pasa por los puntos de intersección de m con la circunferencia de autoinversión y por el centro de inversión C1.
Nos podíamos ahorrar todos los pasos, ya que ahora hay que hacer lo descrito al comienzo del ejercicio, calcular la intersección de las mediatrices de los segmentos que unen los puntos.
Hacemos la circunferencia tangente común f a las inversas: e' d' y a la c. de autoinversión C.
La inversa de f es f', la solución.
-----------------------------------------------------------------------------------------------------
Si en este ejercicio en el paso 3 hacemos las tangentes interiores y exteriores obtenemos 4 circunferencias. Para simplificar, en los siguientes ejercicios haremos generalmente solo las tangentes exteriores.
Dadas 2 circunferencias amarillas a b y un punto P, se trata de hacer todas las circunferencias tangentes a ab y que pasen por P. Cogemos como centro de inversión el punto P y haciendo una recta tangente a una de las circunferencias, por ejemplo a la b, tenemos el radio de la circunferencia de autoinversión auto (en verde) y hacemos centro en P tomando como radio el tamaño de esa tangente. La inversa de b es ella misma y la de a es f. Las tangentes exteriores t1 t2 a las dos inversas f b tienen como inversas e (en verde) d (en azul). Las tangentes interiores t3 t4 tienen como inversas m (en rojo) c (en siena).
-----------------------------------------------------------------------------------------------------
Este es el mismo ejercicio que el anterior pero para que se vea más claro en el paso 3 hacemos solo las tangentes exteriores, por lo que obtenemos 2 circunferencias.
Escogemos el centro de inversión: P y la circunferencia de autoinversión: en color azul llamada C.Autoin.
Hacemos las inversas de los datos: Bi y Ai que se autotransforma en sí misma.
Inversas de las tangentes: M y N, que son la solución.
-----------------------------------------------------------------------------------------------------
Este es otro ejemplo igual que el anterior haciendo sólo las tangentes exteriores, por lo que obtenemos 2 circunferencias.
Hacemos las inversas de los datos: b’ y a que se autotransforma.
-----------------------------------------------------------------------------------------------------
Circunferencia tangente a 1 recta a, y que pase por 2 puntos P y O.
-----------------------------------------------------------------------------------------------------
Circunferencias n, m tangentes a otra c, y que pasen por 2 puntos P, O.
Hacemos las inversas de los datos: P’ y c, que se autotransforma.
-----------------------------------------------------------------------------------------------------
Circunferencia tangente a otra c y a una recta a y que pasa por un punto P.
Hacemos las inversas de los datos: a’ y c que se autotransforma.
-----------------------------------------------------------------------------------------------------
Otro ejemplo Pcr:

27- cPr (P de la circunferencia)
Circunferencia tangente a otra y a una recta y que pase por un punto B de la circunferencia.
Circunferencia tangente a otra c y a una recta a y que pasa por un punto B de la circunferencia c.
Escogemos el centro de inversión: B y la circunferencia de autoinversión: auto
Hacemos las inversas de los datos: a' y c'.
Tangente común a las inversas: g
Inversa de la tangente g: la circunferencia amarilla es una solución, la otra la determinaría la inversa de la paralela a g y tangente a la circunferencia verde por el punto diametralmente opuesto a k.
-----------------------------------------------------------------------------------------------------
28- Prr
Circunferencia que pasa por un punto y es tangente a dos rectas.
Circunferencias tangentes a 2 rectas a, b, y que pasen por un punto P.
Escogemos el centro de inversión: P y la circunferencia de autoinversión: auto
Hacemos las inversas de los datos: a’ y b’
Tangentes comunes a las inversas: t1 y t2
Inversas de las tangentes: m y n, que es la solución.

-----------------------------------------------------------------------------------------------------
29- ccr
Circunferencias tangentes a una recta IG y a dos circunferencias azules BD.
Necesitamos transformar una de las circunferencias en un punto -por ejemplo la D-, para ello le restamos la medida del radio y de esta forma la circunferencia D se transforma en el punto C. Le restamos también a la circunferencia B la misma longitud del radio obteniendo la circunferencia E y de la misma forma le quitamos la misma distancia a la recta en cualquiera de las dos direcciones, transformando la recta azul IG en las recta paralela KL.
Escogemos el centro de inversión: C y la circunferencia de autoinversión: circunferencia verde auto
Hacemos las inversas de los datos: la circunferencia E se transforma en sí misma y la recta KL se transforma en la circunferencia amarilla inferior, ya que la inversa de una recta es una circunferencia que pasa por el centro de inversión C y los puntos de intersección MN con ésta.
Tangentes comunes a las inversas: hemos tomado las toscas gentes externas en color azul claro RU y la que pasa por el punto P y esta gente a la circunferencia E.
Inversas de las tangentes: son las dos circunferencias naranjas a las que le restamos el radio y obtenemos la solución, obteniendo las dos circunferencias rosas.
-----------------------------------------------------------------------------------------------------
30- crr
Circunferencias tangentes a otra circunferencia (amarilla) y a dos rectas (a,b).
Seguimos los pasos de los ejercicios anteriores, pero primero transformamos la circunferencia amarilla en un punto, para ello le restamos el radio y se lo restamos también a las rectas dadas a,b, obteniendo de esta forma a'. b'.
Escogemos el centro de inversión: F (el punto en el que se ha transformado la circunferencia amarilla) y la circunferencia de autoinversión: en color siena (color piel).
Hacemos las inversas de los datos: las dos rectas rojas a’ y b’, se transforman en la circunferencia verde y la circunferencia magenta.
Tangentes comunes a las inversas: las dos rectas marrones MN y KA.
Inversas de las tangentes: las circunferencias de color morado y de color rojo.
Con el mismo centro de las últimas circunferencias calculadas les restamos el radio obteniendo las dos nuevas circunferencias azules que efectivamente son tangentes a las rectas dadas y a la circunferencia amarilla dada, ésta es la solución al problema.
-----------------------------------------------------------------------------------------------------
31- El problema de Apolonio por inversión (ccc) : circunferencias tangentes a otras tres.
Se trata de hacer las circunferencias tangentes a 3 dadas, para ello sumamos o restamos el radio de una de ellas a las otras. El ejercicio tiene por tanto 8 soluciones según sumemos el radio o lo restemos a las otras circunferencias en las 4 posibilidades: + -, - +, + +, - -. Sumaremos 2 posibilidades a cada una de las 4 opciones si hacemos las tangentes exteriores o interiores a las inversas en cada una de las opciones.
Dadas las 3 circunferencias amarillas abc, aumentamos el radio de una (de a ) a otra (así b se transforma en b’) y lo restamos a 2 de ellas (c se transforma en c’ y a se transforma en a’), hasta que quede convertida en un punto una de ellas (a’), convirtiendo el ejercicio prácticamente en uno parecido a los anteriores.
Se coge a’ como centro de inversión y se hacen las tangentes (h) a b’.
La distancia h es el radio de la circunferencia de autoinversión, para que se transforme en sí misma. La inversa de c’ es i.
Hacemos las tangentes interiores t1, t2 a las dos inversas (b’ e i) y las inversas de estas tangentes son y, x.
Aumentando el radio que transformaba a en a’, tenemos la solución x’ y’.

-----------------------------------------------------------------------------------------------------
32- ccc
Dadas las circunferencias m n ñ, para hallar las tangentes, restamos el radio de una de ellas (de m) a las demás. Cogemos el centro de m transformado en el punto C como centro de inversión y hacemos la circunferencia de autoinversión “auto”. La inversa de h es ella misma y de g es v. Las tangentes exteriores a las inversas son a b.
Las inversas de las tangentes son t s. Ampliando el radio en ambas tenemos p q, circunferencias tangentes a las dadas.

-----------------------------------------------------------------------------------------------------
33- ccc
Sintetizando y siguiendo el esquema de las anteriores:
Circunferencias dadas: abc.
Las circunferencias bc se transforman en b’ c’ al sumarles el radio de a, mientras que ésta se transforma en un punto.
Escogemos el centro de inversión: centro de a y la circunferencia de autoinversión: auto.
Tangentes comunes exteriores a las inversas: t1 y t2
Inversas de las tangentes: x y.
Ampliamos el radio de a a y tenemos x’. Reducimos el radio de a a y y tenemos y’.

-----------------------------------------------------------------------------------------------------
34- ccc
Circunferencias dadas: abc.
Las circunferencias bc se transforman en c’ b’ al sumarles y restarles respectivamente el radio de a, mientras que ésta se transforma en un punto.
Escogemos el centro de inversión: centro de a y la circunferencia de autoinversión: auto.
Tangentes comunes interiores a las inversas: t1 y t2
Inversas de las tangentes: n’ m’.
Ampliamos el radio de a a m’ y tenemos m. Reducimos el radio de a a n’ y tenemos n.

-----------------------------------------------------------------------------------------------------
35- Circunferencia tangente a otra circunferencia y a dos rectas rectas crr
Tenemos una circunferencia de centro A, y tenemos dos rectas en negrita más oscuro.
Se pide hacer una circunferencia que sea tangente a la dada y a esas dos rectas.
Tomamos el radio de la circunferencia dada y se lo restamos ambas rectas obteniendo las dos rectas interiores de color marrón, consideramos el centro A como centro de inversión y la circunferencia dada como circunferencia de autoinversión.
Hacemos las inversas de ambas rectas marrones, una es la circunferencia azul y otra es la circunferencia marrón, hacemos las tangentes a ambas circunferencias y tomamos una de las tangentes - ya que sólo nos piden un caso-, por ejemplo la de la derecha y hacemos la inversa de esa recta, que es la circunferencia IGH, por supuesto tangente a las rectas marrones.
Si tomamos el centro de esta circunferencia y le ampliamos el radio que restamos antes, obtenemos ya la circunferencia tangente a las dos rectas en negrita y al mismo tiempo a la circunferencia dada, con lo que el ejercicio queda resuelto.
-----------------------------------------------------------------------------------------------------------------
36- El ejercicio que vemos ahora es el mismo que está resuelto en el ejercicio anterior, con la salvedad de que se han realizado los cuatro casos: las dos circunferencias son tangentes dejando a la circunferencia dada en el interior y luego las otras dos circunferencias también son tangentes a las rectas pero dejando a la circunferencia dada en el exterior.
En el primer caso, como en el ejercicio anterior, le restamos los radios interiormente y por tanto obtenemos las dos circunferencias que dejaron la circunferencia dada en el interior, mientras que en el segundo caso ampliamos el radio a las dos rectas dadas en negrita obteniendo las nuevas rectas azules, hacemos las inversas de estar rectas azules, luego sus tangentes y al final las inversas de las tangentes obteniendo circunferencias tangentes a las azules y que pasan por el centro de inversión, ahora, en este caso les restamos el radio a las circunferencias obtenidas, de esta manera acabamos obteniendo las dos soluciones de las circunferencias interiores, que quedan en color violeta y en color verde.
-------------------------------------------------------------------------------------------------------------
Otros ejemplos de inversión siguiendo los 4 pasos:
Prr:
Pcc:
PPr:
Pcc:
Pcc:
Pcr:
PPc:
Pcr:
ccP:
Pcc:
PPc:
Pcr:
37- La inversión conserva las tangentes:
Parábolas de focos C, D, E, F, G, ...etc., y Directriz (eje y) tangentes todas a la bisectriz del primer cuadrante (de ecuación y =x) y sus inversas en el mismo color correspondiente respecto a la circunferencia de inversión amarilla. Sus inversas son también tangentes a la misma bisectriz.
Para visualizarlas mejor aparecen sus simétricas coloreadas respecto al eje y a la izquierda de la figura.
-----------------------------------------------------------------------------------------------------
38- La inversión conserva los ángulos:
Dadas dos rectas (en color magenta y azul) que forman un ángulo de 32,87° y cuyo vértice del ángulo es G, tenemos su punto inverso F respecto a la circunferencia de autoinversión amarilla de centro A.
Las inversas de ambas rectas son las respectivas circunferencias del mismo color. Si por el punto inverso F de intersección de ambas circunferencias hacemos las dos rectas tangentes a ambas circunferencias, podemos comprobar que se cortan bajo un mismo ángulo de 32,87°. En consecuencia si 2 elementos se relacionan bajo cierto ángulo, sus elementos inversos lo hacen también bajo ese mismo ángulo.
-----------------------------------------------------------------------------------------------------
39- La circunferencia es la única curva que conserva su forma, si entendemos la recta como circunferencia de radio infinito
En la figura podemos ver en color naranja la circunferencia de autoinversión, podemos observar que transforma circunferencias en circunferencias por regla general, como por ejemplo la de color siena exterior que se transforma en la tangente interior, observamos la deformación de las elipses amarilla y azul al ser transformadas en el interior de la circunferencia naranja por inversión.
Aunque todas las formas se deforman mediante la inversión, excepto la circunferencia, salvo el caso en el que se transforma en recta en que se puede considerar una circunferencia de radio infinito, todas conservan las tangentes, de esta forma las elipses que son tangentes entre sí y lo son también a la circunferencia, al hacer sus inversas obtenemos que también las nuevas figuras que salen conservan la inversión. Podemos observar en el dibujo también que la recta que pasa por el centro de la circunferencia e de color siena (color piel) se transforma en la circunferencia e', como podemos observar el centro de la circunferencia no es un invariante proyectivo en la inversión, esto quiere decir que el centro S se transforma en un punto S' que no es el centro de la circunferencia inversa.
Observamos también la tangencia entre rectas y circunferencias, por ejemplo, la recta de color roja m es tangente a la elipse, por tanto su inversa que es la circunferencia verde es tangente también a la inversa de la elipse (la figura azul con forma de haba dentro de la circunferencia de autoinversión).
-----------------------------------------------------------------------------------------------------
40- El Dupin cyclide
El Dupin cyclide como inversa del cilindro (toro de radio infinito) y sus proyecciones ortogonales respectivas: cadena de Steiner que se transforma en circunferencias tangentes alineadas.
Si consideramos el dibujo inferior con elementos tridimensionales, tenemos lo siguiente: a la derecha un cilindro que contiene esferas de distintos colores, amarilla, azul, naranja, etc.
La circunferencia de autoinversión se transforma en una esfera de autoinversión mientras que el cilindro que es tangente a la esfera en un punto se transforma en una figura parecida a un toro que se va estrechando cada vez más hasta que en el centro del esfera de a autoinversión se transforma, en este caso, en un punto. Tenemos entonces que en este toro transformado como en un neumático abultado por un lado más que por otro contiene también en su interior a esferas tangentes al mismo, que son asimismo inversas de las esferas del cilindro. Este toro deformado se llama Dupin cyclide.
Al proyectar ambos elementos sobre un plano, el Dupin cyclide con sus esferas tangentes interiores y el cilindro de esferas de colores, se transforman respectivamente en la cadena de Steiner y en las circunferencias de colores situadas en la columna vertical tangente a la circunferencia de autoinversión.
-----------------------------------------------------------------------------------------------------
41- Construcción de la cadena de Steiner por inversión:
La cadena de este Steiner está formado por dos circunferencias no concéntricas que contienen en su interior a otras circunferencias tangentes entre sí, tal y como parece a la izquierda en el dibujo.
Para construirla podemos dibujar un polígono regular como el de la derecha del dibujo, que contenga el mismo número de vértices que circunferencias tangentes interiores va a tener la cadena. Dibujamos a continuación las circunferencias tangentes que tienen un radio igual a la mitad del lado del polígono y tienen por centros los distintos vértices del polígono. Por último dibujamos las dos circunferencias concéntricas interior y exterior a las cinco circunferencias dibujadas previamente.
Para construir la cadena dibujamos un centro A que va a ser el de inversión, y una circunferencia de autoinversión. Aplicamos la inversión de todos los elementos dibujados anteriormente y obtenemos la cadena de Steiner.
42- Como podemos comprobar los centros de las circunferencias no son invariantes tras la transformación inversa, pero sí lo son las tangentes, los puntos de tangencia y la ordenación de las figuras.
-----------------------------------------------------------------------------------------------------
43- Figura inversa de un damero infinito en extensión o malla de cuadrados:
A continuación tenemos un damero infinito o embaldosado de figuras cuadradas alternas entre blanco y naranja. Como podemos observar el embaldosado contiene cuadriláteros cuyos lados son por regla general circunferencias excepto cuando pasan por el centro de inversión, en este caso se transforman en rectas.
Figura anterior en blanco y negro:
-----------------------------------------------------------------------------------------------------
45- Inversa de rectángulos
Conjunto de rectángulos azules que se transforman en cuadriláteros rojos cuyos lados son por regla general curvos, salvo aquellos que corresponden a las líneas de los lados que pasan por el centro de inversión. Los dos espacios (cuadriláteros azules y cuadriláteros rojos) están perfectamente acotados por el límite de la circunferencia del autoinversión (de color verde).
-----------------------------------------------------------------------------------------------------
46- Inversa de una malla de triángulos equiláteros:
Al igual que en la figura anterior los triángulos equiláteros contienen lados que se transforman por regla general en circunferencias excepto cuando éstos lados pasan por el centro de inversión, en cuyo caso las figuras transformadas son triángulos cuyos lados son rectos.
-----------------------------------------------------------------------------------------------------
47- Inversa de una malla de franjas paralelas
El conjunto de franjas amarillas paralelas se transforma por inversión en un conjunto de arcos de circunferencia también alternos entre el blanco y el amarillo oscuro.
-----------------------------------------------------------------------------------------------------
48- Inversa de las líneas de una figura con formas amarillas y azules
Sus inversas son las figuras con colores verdes y naranjas, aunque los colores de las inversas no son correspondientes a los colores de las originales. Un ejercicio podría consistir en corregir los colores para que exista inversión en líneas y colores.
He aquí la solución:
-----------------------------------------------------------------------------------------------------
49- El infinito en la inversión

En la figura podemos observar las inversas de una parábola, una hipérbola y una circunferencia. Como la parábola y la hipérbola tienen un punto en el infinito el inverso de éste es el centro de inversión, tenemos que ambas figuras Inversas de dadas pasan por ese punto, en el caso de la parábola es una curva con forma aerodinámica de color azul con el punto de retroceso A en el inverso del infinito o centro de inversión, mientras que en el caso de la hipérbola, como una de las ramas de la hipérbola va hasta el infinito y vuelve por el otro lado hacia la otra rama tenemos que ambas están conectadas en el punto del infinito por tanto la inversa es una curva con forma de elipse pero algo más lenticular que va hasta el infinito y en ese punto doble A aparece la nueva curva inversa de la otra rama de la hipérbola. Observamos también que las dos verticales tangentes a ambas curvas se transforman en dos circunferencias tangentes en el inverso del infinito o centro de inversión.
-------------------------------------------------------------------------------------------------
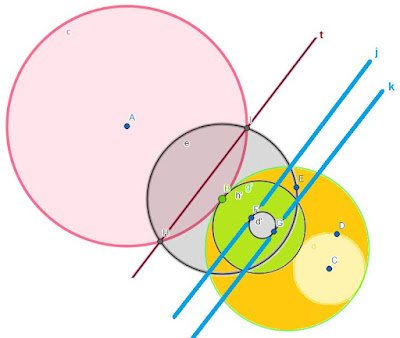
50- Cisoide de Diocles (curva verde d'), inversa de parábola (curva roja d)
En la figura podemos observar la cisoide de Diocles, para trazarla podemos dibujar los puntos inversos de una parábola y obtenemos la curva verde o cisoide, el punto de intersección de la parábola con la circunferencia de auto inversión será un punto de la cisoide mientras que el vértice de la parábola que pasa por el centro de la circunferencia de otra inversión será el vértice de la curva cisoide.
Respecto a la asíntota que pasa por el punto N y que es ortogonal al eje de simetría, podemos hacer una circunferencia que pase por los puntos AN, siendo este segmento su diámetro, si trazamos aleatoriamente una recta j que pasa por el centro de inversión A, está recta corta a la circunferencia y asíntota en QP -segmento de color rosa-, tomamos esta distancia -en el dibujo indicado por el segmento de color magenta- desde el centro de inversión con la misma longitud del segmento hasta que corte a la recta j, tenemos así un punto R de la curva cisoide.
El mismo procedimiento se repite con la recta AS por debajo del eje x, como podemos observar campos segmentos azules son iguales, la distancia AT desde el centro la curva como la distancia US.
---------------------------------------------------
51- Inversa de pentágono regular y pentagrama:
Como cualquier figura inversa, según se va acercando al centro de inversión se va reduciendo en tamaño, ya que la inversión transforma todo el plano que está fuera de la circunferencia en lo que queda dentro de la circunferencia, de manera que el infinito del plano se convierte en el centro de inversión, y lo que está muy alejado aparece cerca del centro de inversión.
Inversas de pentágonos:
-----------------------------------------------------------------------------------------------------
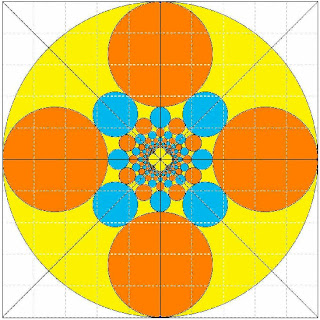
52- Inversas de círculos tangentes:
En este caso, las circunferencias originales tangentes de las que se realiza sus inversas, tienen sus centros situados en los vértices de triángulos equiláteros, en consecuencia, los huecos entre circunferencias son "triángulos" de lados curvos.
Un cuadrante:
Circunferencia completa con estructura de circunferencias tangentes circundante:
Circunferencia autoinversa con elementos inversos (detalle ampliado del dibujo anterior):
-----------------------------------------------------------------------------------------------------
53- Inversa de circunferencias tangentes:
En este caso, las circunferencias originales tangentes de las que se realiza sus inversas, tienen sus centros situados en los vértices de cuadrados, en consecuencia, los huecos entre circunferencias son "cuadrados" de lados curvos.
-----------------------------------------------------------------------------------------------------
54- Inversa de una figura:
En la figura observamos en el centro una circunferencia con varios cuadrados y circunferencias con los distintos colores: azul, rojo y amarillo. Fuera de este círculo aparecen las figuras inversas de todos estos elementos, el azul saturado se convierte en un azul más claro en su inversa, lo mismo le ocurre al amarillo que se transforma en una tonalidad ocre claro y el rojo que se transforma en color naranja.
En la figura podemos observar con más detalle en uno de los cuadrantes que el cuadrado se transforma en esta figura en forma de delta:
Recíprocamente, la forma de delta se transforma por inversión en el cuadrado.
-----------------------------------------------------------------------------------------------------
55- Inversa de una malla de módulos hexagonales
Resultado de invertir la red de piezas hexagonales anterior:
-----------------------------------------------------------------------------------------------------
56- Teselación e inversa
Simetría axial doble de la figura anterior
Detalle del ejercicio anterior:
57- Inversa de la teselación anterior pero sin simetría axial de los cuadrantes:
La inversas de la teselación son simétricas entre sí respecto al centro de inversión (simetría central).

-----------------------------------------------------------------------------------------------------
Más ejemplos de estructuras geométricas (a la derecha) y sus formas inversas (a la izquierda):
Geometría de líneas rectas que se transforman por inversión en la estructura central de circunferencias de colores.
Resultado final aplicable a distintos diseños.

-----------------------------------------------------------------------------------------------------
58- crP
Dada la circunferencia W
y la recta s, además del punto B perteneciente a la circunferencia W. Se pide calcular dos
circunferencias tangentes a la circunferencia W y recta s, que pasen por el
punto B.
Tomamos el punto B como
centro de inversión y hacemos una circunferencia de autoinversion con un
radio cualquiera que llamaremos E.
Hacemos las inversas de
la circunferencia W y de la recta S.
Esas inversas son la
recta i y la circunferencia pequeña v.
Hacemos las
tangentes a la circunferencia v y a la recta i que serán las dos rectas
azules ñ k, tangentes a la circunferencia v y que siguen la dirección de la
recta i.
Las inversas de esas dos
circunferencias azules son las dos circunferencias amarillas m y n que son la
solución ya que ambas son tangentes a los dos elementos dados por el punto B.
----------------------------------------------------------------------------------------------------
59- ccP
Dadas dos circunferencias en color rosa y amarillo, de centro A y centro C respectivamente, además de un
punto verde B, sobre la circunferencia rosa.
Se pide hacer dos circunferencias tangentes a ambas circunferencias dadas y
que pasen por el punto B
Tomamos el punto B como
centro de inversión y hacemos una circunferencia e de radio cualquiera que
llamaremos de autoinversion, en el dibujo de color gris
Hacemos las inversas de
ambas circunferencias que son la recta t y la circunferencia pequeña de color gris
llamada d’
Hacemos las tangentes a
ambos elementos, éstas tangentes son las rectas de color azul que siguen
la dirección de la recta t y son tangentes a la circunferencia pequeña de color
gris d’
Las inversas de estas
dos rectas azules son las dos soluciones, esto es la circunferencia naranja y
la circunferencia verde.
-----------------------------------------------------------------------------------------------------
60- PRR
Tenemos dos rectas azules BE y un punto D en color rojo, se pide hacer las circunferencias tangentes a
las rectas azules y que al mismo tiempo pasen por el punto rojo D.
1- Tomamos el
punto rojo D como centro de inversión y hacemos una circunferencia rosa c
de radio aleatorio, dibujamos las inversas de ambas rectas azules
obteniendo las dos circunferencias
negras que pasan por D.
Hacemos las rectas
tangentes rojas a las circunferencias negras y a continuación las inversas de
esas dos tangentes, que son las circunferencias verdes, la solución.
2- En el caso dos
vemos exactamente el mismo ejercicio pero las rectas azules tienen un ángulo
mayor por lo que es menos intuitivo, por ello se pone este ejemplo para
que en caso de que resulte difícil resolverlo se consideren casos particulares
como éste donde se pueda ver de forma más concreta la solución.
En el número uno las
circunferencias verdes aparecen más pequeñas y se ven completas en la
imagen, mientras que en el número dos hay una circunferencia verde muy
grande por lo que resulta menos intuitivo y de más difícil comprensión,
podemos resolver el segundo si tenemos problemas para encontrar la solución,
cambiando el ángulo de las rectas azules de manera que quede
como el ejercicio
1.
------------------------------------------------------------------------------------------------------
61- crr
Tenemos en este caso (1 y 2) las circunferencias tangentes a dos rectas en color color rojo y a una circunferencia también en color rojo.
1- En el primer caso hacemos dos paralelas verdes a las rectas dadas pero por la parte externa y que tengan de distancia la misma longitud del radio de la circunferencia roja dada.
Reducimos la circunferencia roja dada a un punto que es el centro de inversión y tomamos esa misma circunferencia como la de puntos dobles o puntos que son inversos de sí mismos.
Seguimos el proceso de siempre, esto e,s hacemos las inversas de las rectas verdes, luego las tangentes de esas circunferencias inversas y luego las inversas de las tangentes que son las circunferencias marrones.
Haciéndolo luego circunferencias concéntricas a estas marrones, pero restando el radio de la dada roja, obtenemos las dos soluciones de las circunferencias que, siendo tangentes a las rectas dejan a la circunferencia roja por fuera y son tangentes también a ella.
2- El segundo caso señalado con el número dos es idéntico al anterior pero en vez de coger las tangentes exteriores en color verde pues cogemos las interiores y a continuación también reducimos la circunferencia a un punto que será el centro de inversión y cogemos la misma circunferencia roja como de autoinversión.
Procediendo con los pasos que utilizamos siempre, o sea, las inversas de las rectas verdes y las tangentes a esas circunferencias y las inversas de éstas, nos dan las circunferencias menores tangentes a las verdes. A continuación hacemos las circunferencias concéntricas a esas menores hasta que sean tangentes a las rectas rojas dadas.
Como podemos ver en la solución las nuevas circunferencias grises son tangentes a las rojas y a la circunferencia roja pero esta vez dejan a la circunferencia dentro.
-------------------------------------------------------------------------------------------------------
62- Problema combinado de tangencias por inversión y de arco capaz.

El ángulo mayor bajo el que se ve el segmento CE desde un punto de la recta a es H, punto de tangencia de la circunferencia que pasa por CE y tangente a la recta a.
Si nos alejamos por la recta el ángulo será menor por estar más lejos del segmento que si pertenece el punto a la circunferencia, cuyo ángulo es igual al visto desde H. En base a ello se puede realizar el siguiente ejercicio:
Si nos movemos por el segmento azul, se pide calcular el punto desde el cual observamos el segmento AB bajó un ángulo máximo.
Construimos una circunferencia de autoinversión de centro A, en el dibujo en color rosa. Para mayor facilidad en la ejecución del ejercicio hacemos que esta circunferencia sea tangente a la recta dada azul. Calculamos la inversa de esta recta que es la circunferencia del centro F y diámetro EA. Calculamos también el inverso del punto B, que es B’.
Hacemos las tangentes B’I y B’K desde este punto B’ a la circunferencia de diámetro EA y tenemos que las inversas de estas tangentes son las dos circunferencias tangentes a la recta azul (en el dibujo en color verde). Los puntos de tangencia de estas circunferencias con la recta azul son los puntos desde los que se ve el mayor ángulo el segmento AB.
Podemos desplazar el punto N y comprobar efectivamente que desde cualquier punto de la recta distinto se ve el segmento bajo un ángulo menor.
Según el
arco capaz, todos los puntos de la circunferencia verde comprenden el segmento bajo el mismo ángulo, esto quiere decir que si N se desplaza por la circunferencia verde el ángulo es invariable. Para verificar que esto es cierto se ha cogido un punto cualquiera O de la circunferencia desde el que se han trazado dos rectas a los puntos AB, observamos que las dos líneas OA y OB forman también el mismo ángulo 35,04°.
tangencias por inversión y arco capaz. - GeoGebra Hoja Dinámica-->